Statics of Rigid Bodies

Bending Moments

Definition: Bending Moment can be defined as the product of a force \((F)\) and a moment arm \((d)\). The moment arm is the perpendicular distance from the axis \((y)\) at the moment center \((o)\) to the line of action of the force. Refer to the figure.
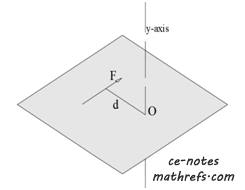
statics-moment-arm

Thus: \(M_o = Fd\)

Another way of visualizing the moment is by considering it as twice the area of the triangle formed by connecting the endpoints of the force vector, \(F\), to the moment center\((o)\), with the apex at the moment center.Refer to the Figure.

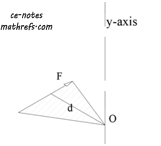
statics-moment-arm

\(M_o = 2A_t = 2 [\dfrac{Fd}{2}]\)

\(M_o = 2A_t = Fd\)

The moment unit, obtained by multiplying force by distance, is commonly stated in lb-ft, N-m, KN-m, gm-cm, or other comparable units, which represent the combination of force and distance. Since moment creates a rotational motion around an axis, engineers often define counterclockwise as negative and clockwise as a positive.