Statics of Rigid Bodies

---

Varignon's Theorem

---

Varignon’s Theorem states that the moment of a force is equivalent to the sum of the moments of its components. This can be demonstrated using the figure .

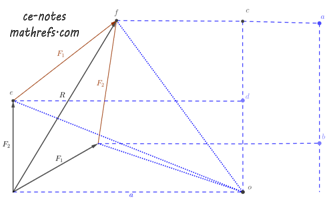
Let \(F_1\) and \(F_2\) be concurrent forces and \(R\) be their resultant. Since \(R\) is the resultant we can represent \(F_1\) and \(F_2\) as \(R\) and the moment at point \(O\) will be \(M_o=Rd\).

Since, we defined that the moment is twice the area of the triangle made by connecting the endpoints of the force vector to the moment center. Thus, to prove Varignon’s theorem we need to show that the sum of the area of the triangle formed by connecting \(F_1\) to the moment center and the triangle formed by connecting \(F_2\) to the moment center is the same as the area of the triangle formed when we connect endpoints of \(R\) to the moment center \((o)\).

Area of triangle formed by connecting \(F_1\) to \(o\)

\(A_{F_1} = \dfrac{a(ob)}{2}\)

Area of triangle formed by connecting \(F_2\) to \(o\)

\(A_{F_2} = \dfrac{a(od)}{2}\): But \(od =ab\)

\(A_{F_2} = \dfrac{a(ab)}{2}\)

---

---

Area of triangle formed by connecting \(R\) to \(o\)

\(A_R=\dfrac{(a)oc} {2}\): But \(oc=ob+ab\)

\(A_R=\dfrac{1}{2} (a)(ob+ab)\)

\(A_R=\dfrac{1}{2} (a)(ob)+ \dfrac{1}{2} (a)(ab)\)

\(A_R=A_{F_1} +A_{F_2}\), thus the theorem is true.

---