Statics of Rigid Bodies
Resultant Forces
Definition:The Resultant force is the sum of all forces acting on an object. We often used sign conventions to denote Downard (-) and Upward forces (+).
Resultant of a Rectangular Load
A rectangular load \((𝑤)\) is in weight per length, for SI units that would be typically in \(\dfrac{KN}{m}\) or \( \dfrac{N}{m}\). To compute the Resultant we get the area of the rectangle. Using the figure below, the resultant would be \(R = w(L)\)
Location of the Resultant in a Rectangular Load
The location of the resultant can be calculated using Varignon’s Theorem , which states that the moment of the resultant is the same as the summation of the moment of the components. In a rectangular loading there are a lot of vertical loads (components), and we need to sum all the moments of those components.
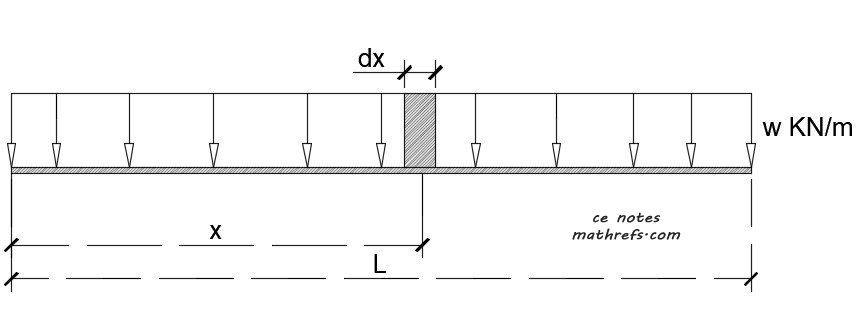
We can take one rectangular component with a width of \(dx\), at a variable distance \(x\) from the left edge. Applying the theorem we have;
\[ x_R R = \sum {F_c (x_c)}\]
\[x_R(wL) = \int_{0}^{L}{(w dx)} (x)\]
\[x_R = \dfrac{1}{wL} (w) (\dfrac{x^2}{2})]_0^L \]
\[x_R = \dfrac{L^2}{2L}\]
\[x_R = \dfrac{L}{2}\]
Thus, the location of the Resultant in a rectangular Load is at the middle of the span.
Resultant of a Triangular Loads
The presultant (R) of a triangular load is the area of the triangle. Using the figure below, \(R =\dfrac{wL}{2}\)
Location of the Resultant in a Triangular Load
The location of the resultant can be calculated using Varignon’s Theorem , which states that the moment of the resultant is the same as the summation of the moment of the components. Refer to the figure.
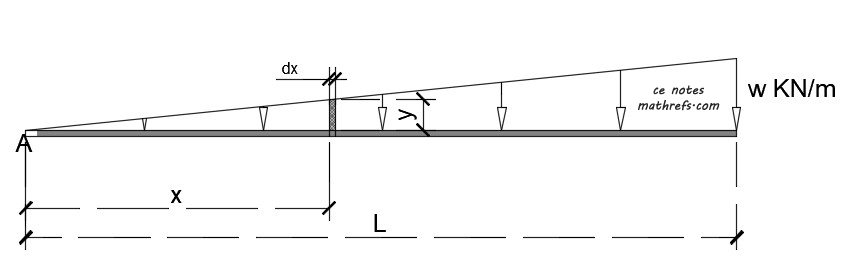
For a triangular loading, we can get a rectangular component with a width of \(dx\) and a height \(y\) at a variable distance \(x\). With the same principle we have,
\[ x_R (R) = \sum{F_c d_c}\]
\[(x_R) \dfrac{wL}{2} = \int_{0}^{L} {ydx} (x)\]: the \(ydx\) is the area of each component and \(x\) is it's moment arm.
By ratio and proportion we have \[\dfrac{w}{L} = \dfrac{y}{x}\]
\[y= \dfrac{w}{L} (x)\]
\[x_R = (\dfrac{2}{wL}) (\dfrac{w}{L}) \int_{0}^{L} {(x)(x)dx}\]
\[x_R = (\dfrac{2}{L^2}) \dfrac{x^3}{3} |_0^L\]
\[x_R = (\dfrac{2}{L^2}) \dfrac{L^3}{3} \]
\[x_R = \dfrac{2}{3} L \]
Thus, the Resultant of a triangular load is located at \(\dfrac{2}{3} L\) from \(0\) load of the triangle. From the right angle of the triangle that would be \(L -\dfrac{2}{3} l = \dfrac{1}{3}L\)